Data Structure Interview

What is the difference between an array and a linked list?

• Array:

  • Fixed size (in most languages)
  • Contiguous memory allocation
  • Fast random access
  • Insertion/deletion is expensive (except at the end)

• Linked List:

  • Dynamic size
  • Non-contiguous memory allocation
  • Slow random access
  • Fast insertion/deletion

Explain the difference between a stack and a queue.

• Stack:

  • Last-In-First-Out (LIFO) structure
  • Push (insert) and pop (remove) operations occur at the same end
  • Used for function calls, undo mechanisms, expression evaluation

• Queue:

  • First-In-First-Out (FIFO) structure
  • Enqueue (insert) at rear, dequeue (remove) from front
  • Used for task scheduling, breadth-first search

What is a binary search tree?

A binary search tree is a binary tree data structure where each node has at most two children, referred to as the left child and the right child. For each node:

• All nodes in the left subtree have values less than the node’s value
• All nodes in the right subtree have values greater than the node’s value

This property allows for efficient searching, insertion, and deletion operations.

Explain the concept of hashing and hash tables.

Hashing is a technique used to uniquely identify a specific object from a group of similar objects. It involves using a hash function to map keys to indices of an array (hash table).

Hash Table:

• Data structure that implements an associative array abstract data type
• Uses a hash function to compute an index into an array of buckets or slots

What is a balanced tree and why is it important?

A balanced tree is a binary tree structure in which the left and right subtrees of every node differ in height by no more than one. Examples include AVL trees and Red-Black trees.

Importance:

• Ensures O(log n) time complexity for operations like insertion, deletion, and search
• Prevents degeneration into a linked list, which would result in O(n) time complexity

Explain the difference between DFS and BFS.

• Depth-First Search (DFS):

  • Explores as far as possible along each branch before backtracking
  • Uses a stack (or recursion)
  • Memory efficient for trees
  • Can get trapped in infinite loops for graphs

• Breadth-First Search (BFS):

  • Explores all the neighbor nodes at the present depth prior to moving to nodes at the next depth level
  • Uses a queue
  • Finds the shortest path in unweighted graphs
  • Can be memory-intensive

What is a heap data structure?

A heap is a specialized tree-based data structure that satisfies the heap property:

• In a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C
• In a min heap, the key of P is less than or equal to the key of C

Heaps are commonly used to implement priority queues and in sorting algorithms like heapsort.

Explain the concept of dynamic programming.

Dynamic programming is both a mathematical optimization method and a computer programming method. It works by breaking down a complex problem into simpler subproblems in a recursive manner.

Characteristics:

• Overlapping Subproblems
• Optimal Substructure

Common examples:

• Fibonacci sequence
• Longest Common Subsequence
• Knapsack problem

What is a trie and what is it used for?

A trie, also called digital tree or prefix tree, is a kind of search tree—an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings.

Uses:

• Autocomplete
• Spell checkers
• IP routing tables
• Solving word games

Explain the concept of a self-balancing tree.

A self-balancing tree is a type of binary search tree that automatically keeps its height small in the face of arbitrary insertions and deletions. This ensures that operations like search, insert, and delete take O(log n) time.

Examples:

• AVL trees
• Red-Black trees
• Splay trees

These trees use rotations to maintain balance after insertions and deletions.

What is the time complexity of common operations in different data structures?

• Array:

  • Access: O(1)
  • Search: O(n)
  • Insertion: O(n)
  • Deletion: O(n)

• Linked List:

  • Access: O(n)
  • Search: O(n)
  • Insertion: O(1)
  • Deletion: O(1)

• Binary Search Tree (balanced):

  • Search: O(log n)
  • Insertion: O(log n)
  • Deletion: O(log n)

• Hash Table:

  • Search: O(1) average, O(n) worst
  • Insertion: O(1) average, O(n) worst
  • Deletion: O(1) average, O(n) worst

Explain the concept of a graph and its representations.

A graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph.

Representations:

• Adjacency Matrix: 2D array of size V x V where V is the number of vertices
• Adjacency List: Array of linked lists
• Edge List: List of all edges in the graph

What is the difference between a min-heap and a max-heap?

• Min-Heap:

  • The root node has the minimum value
  • For any given node C, if P is a parent node of C, then the key of P is less than or equal to the key of C

• Max-Heap:

  • The root node has the maximum value
  • For any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C

Both are commonly used to implement priority queues.

Explain the concept of a B-tree.

A B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. It is optimized for systems that read and write large blocks of data.

Properties:

• All leaves are at the same level
• A non-leaf node with k children contains k-1 keys
• Each node (except root) must contain at least t-1 keys, where t is the minimum degree of B-tree
• All nodes may contain at most 2t-1 keys

B-trees are commonly used in databases and file systems.

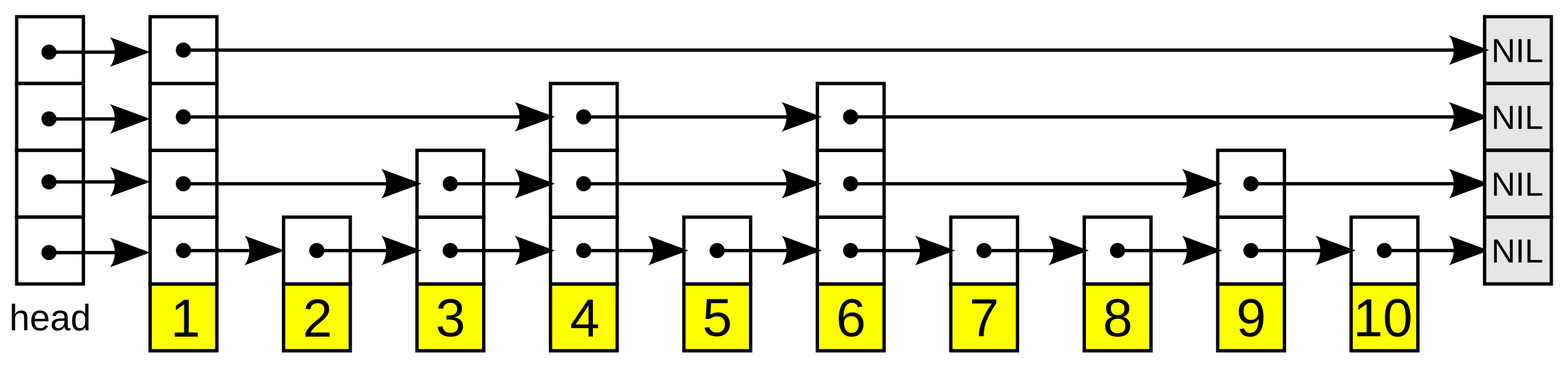
What is a skip list?

A skip list is a probabilistic data structure that allows O(log n) search complexity as well as O(log n) insertion complexity within an ordered sequence of elements. It is created from a linked list by adding multiple layers of header nodes.

Advantages:

• Performs as well as balanced trees
• Simpler to implement than balanced tree structures

Explain the difference between internal and external sorting.

• Internal Sorting:

  • All data to be sorted is held in main memory
  • Faster but limited by available RAM
  • Examples: Quicksort, Mergesort, Heapsort

• External Sorting:

  • Used when data doesn’t fit into main memory and must reside in slower external memory (like a hard drive)
  • Involves multiple steps, often using merge sort
  • Example: External merge sort

What is a bloom filter?

boom_filters

Explain the concept of a disjoint-set data structure.

A disjoint-set data structure, also called a union-find data structure, keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets.

Operations:

• Find: Determine which subset a particular element is in
• Union: Join two subsets into a single subset

Uses:

• Kruskal’s algorithm for finding minimum spanning trees
• Detecting cycles in graphs

Path compression optimization